背包九讲

背包问题

https://www.cnblogs.com/jbelial/articles/2116074.html

• • 背包问题
    • 01 背包问题
    • 完全背包问题
    • 多重背包问题
    • 混合背包问题
    • 二维费用的背包问题
    • 分组背包问题
    • 有依赖的背包问题
    • 背包问题求方案数
    • 求背包问题的方案

01 背包问题

https://www.acwing.com/problem/content/2/

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。第 $i$ 件物品的体积是 $v_i$，价值是 $w_i$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

注意的点：

• 空间优化：使用一个一维数组即可，每次保存上一层的计算结果，然后从后往前计算(保证逻辑等价即可)。
• 如果考虑体积恰好等于 $V$ 的最大价值，只需要将 $f[0][0]$ 初始化为 0，$f[0][j\neq 0]$ 初始化为负无穷，保证如果结果不是从 $f[0][0]$ 递推出来的为负无穷，最后判断最大的结果 $\max\{f[n][m=0,1...n]\}$

#include<iostream>

using namespace std;

const int N=1010;
int v[N], w[N];
int f[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i];
        
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])
                f[i][j] = max(f[i-1][j], f[i-1][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m]<<endl;
}

完全背包问题

https://www.acwing.com/problem/content/3/

有 $N$ 种物品和一个容量是 $V$ 的背包，每种物品都有无限件可用。第 $i$ 种物品的体积是 $v_i$，价值是 $w_i$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

• 优化空间化的形式与 01 背包相似，体积循环的方向从小到大

/**
 * 1. 01背包   f[i][j]=max(f[i-1][j], f[i-1][j-v]+w);
 * 2. 完全背包 f[i][j]=max(f[i-1][j], f[i][j-v]+w);
 * 
 */

#include<iostream>

using namespace std;
const int N=1010;

int n,m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin>>n>>m;
    
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            f[i][j] = f[i-1][j];
            if(j>=v[i])
                f[i][j]=max(f[i][j], f[i][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

多重背包问题

https://www.acwing.com/problem/content/4/

有 $N$ 种物品和一个容量是 $V$ 的背包。第 $i$ 种物品最多有 $s_i$ 件，每件体积是 $v_i$，价值是 $w_i$。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

#include<iostream>
using namespace std;

const int N=110;
int n,m;
int f[N];

int main()
{
    cin>>n>>m;
    for(int i=1; i<=n; i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        // 优化同01背包
        for(int j=m; j>=0; j--)
            for(int k=1; k<=s && k*v <=j; k++)
                f[j]=max(f[j], f[j-k*v]+k*w);
    }
    cout<<f[m]<<endl;
    return 0;
}

注意的点：

• 二进制优化方法：如果 $S$ 范围较大，可以将 $S$ 用 $\lfloor{log_2S}\rfloor+1$ 个数来表示 (即二进制 $1,2,4...$ 划分，但是不能超界)，然后使用 01 背包问题求解。复杂度 $O(NVlnS)$ 题目和代码

• 单调队列优化方法：将循环的体积分为 $v$ 类，使用单调队列优化。(算法题中使用 deque 可能会卡常数，使用数组模拟) 题目和代码

单调队列优化方法：

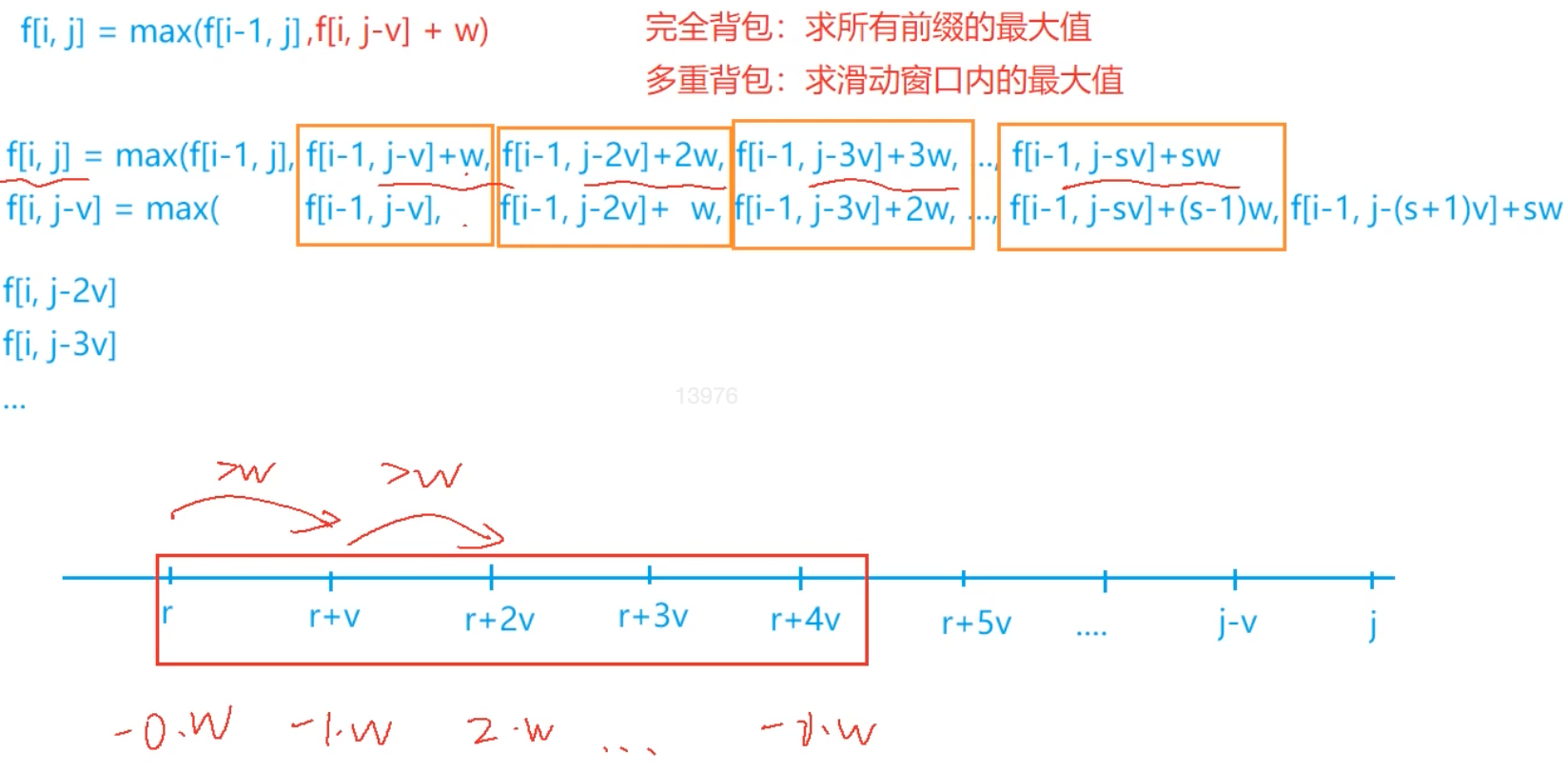
代码：

#include<iostream>
#include<deque>
#include<cstring>
using namespace std;

const int N=20010; //V
int n,m;
int f[N], g[N]; // g[N]作为滚动数组
deque<int> q;

int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        memcpy(g, f, sizeof f);
        for(int j=0; j<v; j++) //remain
        {
            //每次需要重新清空队列
            q.clear();
            for(int k=j; k<=m; k+=v) //遍历j j+v j+2v ...;窗口大小为s
            {
                if(!q.empty() && q.front()<k-s*v) //前s个(不包括k)
                    q.pop_front();
                //先更新结果，f[k]与该元素前s窗口元素的max
                if(!q.empty())
                    f[k]=max(f[k], g[q.front()]+(k-q.front())/v * w);
                //insert
                while(!q.empty() && g[q.back()]-(q.back()-j)/v *w <= g[k]-(k-j)/v *w)
                //while (hh <= tt && g[q[tt]] <= g[k] - (k - q[tt]) / v * w) tt -- ;
                    q.pop_back();
                q.push_back(k);
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

混合背包问题

https://www.acwing.com/problem/content/7/

有 $N$ 种物品和一个容量是 $V$ 的背包。物品一共有三类：

• 第一类物品只能用 1 次（01 背包）；
• 第二类物品可以用无限次（完全背包）；
• 第三类物品最多只能用 $s_i$ 次（多重背包）；

每种体积是 $v_i$，价值是 $w_i$。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

利用二进制优化，全部转换为 01 背包和完全背包，然后求解每一层(列举物品)

二维费用的背包问题

https://www.acwing.com/problem/content/8/

有 $N$ 件物品和一个容量是 $V$ 的背包，背包能承受的最大重量是 $M$。每件物品只能用一次。体积是 $v_i$，重量是 $m_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

二维费用背包问题将限制扩展为两维-体积和重量，思路和 01 背包相同，dp 数组可以省略一维

#include<iostream>
using namespace std;

const int N=110;
int n,v,m;
int f[N][N];

int main()
{
    cin>>n>>v>>m;
    for(int i=0; i<n; i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        for(int j=v; j>=a; j--)
            for(int k=m; k>=b; k--)
                f[j][k]=max(f[j][k], f[j-a][k-b]+c);
    }
    cout<<f[v][m]<<endl;
    return 0;
}

分组背包问题

https://www.acwing.com/problem/content/9/

有 $N$ 组物品和一个容量是 $V$ 的背包。每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 $v_{ij}$，价值是 $w_{ij}$，其中 $i$ 是组号，$j$ 是组内编号。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

思路与 01 背包一样

有依赖的背包问题

https://www.acwing.com/problem/content/10/

有 $N$ 个物品和一个容量是 $V$ 的背包。物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。(依赖关系形成一颗树)
每件物品的编号是 $i$，体积是 $v_i$，价值是 $w_i$，依赖的父节点编号是 $p_i$。物品的下标范围是 $1…N$。求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

树形 DP+分组背包问题

#include<iostream>
#include<cstring>
using namespace std;

const int N=110;
int n,m;
int h[N], e[N], ne[N], idx;
int v[N], w[N], f[N][N];

void add(int a, int b) // add node(b) to head(a)
{
    e[idx]=b, ne[idx]=h[a], h[a]=idx++;
}

void dfs(int u)
{
    for(int i=h[u]; i!=-1; i=ne[i])
    {
        int son=e[i];
        dfs(son); // 更新子节点
        for(int j=m-v[u]; j>=0; j--)
            for(int k=0; k<=j; k++)
                f[u][j]=max(f[u][j], f[u][j-k]+f[son][k]);
    }
    for(int i=m; i>=v[u]; i--) // 容量大于等于根节点需要加上根节点的价值
        f[u][i]=f[u][i-v[u]]+w[u];
    for(int i=0; i<v[u];i++)   // 容量小于根节点的总价值为0
        f[u][i]=0;
}

int main()
{
    memset(h, -1, sizeof h);
    cin>>n>>m;
    int root;
    for(int i=1; i<=n; i++)
    {
        int p;
        cin>>v[i]>>w[i]>>p;
        if(p==-1) root=i;
        else add(p, i);
    }

    dfs(root);
    cout<<f[root][m]<<endl;
    return 0;
}

背包问题求方案数

https://www.acwing.com/problem/content/11/

思路同 01 背包

注意的点：

• 求最大价值的方案数，就是求恰好达到最大价值的方案数，需要将状态 $f[j]$ 理解为前 $i$ 个物品中体积恰好是 $j$ 的最大价值（只需要将初始化 $f[j=0]=0, f[j>=1]=- \infty$，即所有其他状态都是有 $f[0]$ 转移而来的）

• 同时添加方案数组 $g[j]$ 表示体积恰好是 $j$ 的最大价值的方案数。（根据递推关系得到）

for(int j=m; j>=v; j--)
{
    int t=max(f[j], f[j-v]+w);
    int s=0;
    if(t==f[j]) s+=g[j];       // 最大价值转移路径1
    if(t==f[j-v]+w) s+=g[j-v]; // 最大价值转移路径2
    if(s>=mod) s-=mod;
    f[j]=t;
    g[j]=s;
}

• 注意最后最优解是所有 $f[j]$ 的最大价值（因为最优解需要的体积可能小于背包总容量，而且可能是不同的体积）

求背包问题的方案

https://www.acwing.com/problem/content/12/

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。第 $i$ 件物品的体积是 $v_i$，价值是 $w_i$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出 字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 $1…N$。

注意：

• 存储完整的状态 $f[i][j]$

• 根据状态来 $f[n][m]$ 来倒推选择的物品 （是否选择了第 $n$ 件，第 $n-1$ 件，…）

// f[n][m]
// if f[n][m] = f[n-1][m] 不选第n件物品
// if f[n][m] = f[n-1][m-v[n]]+w[n] 选第n件物品

• 由于输出字典序最小的方案，根据贪心，需要优先选择序号小的物品，倒推需要从第 1 件物品开始；
  所以求解问题时从 $N...1$ 的顺序来列举物品（将 1 号物品看成最后一个），最后从 $f[1][m]$ 根据贪心来倒推选择的物品。