纠删码基础

内容：解释和理解伽罗华域和基础的 RS 编码理论，和编码实践。

1. Cauchy or Vandermonde?
2. 写一个Reed-Solomon code引擎
3. 高性能纠删码编码
4. 有限域内的四则运算
5. 分布式系统系列教程之: Erasure-Code

1. 伽罗华域

有关 群、环、域 在之前总结过，这里也有用到的代数基础

范德蒙码和柯西码的译码过程、范德蒙系统码的生成矩阵的构造都需要矩阵求逆运算，柯西码的构造中涉及到求乘法逆元的运算，这些运算在实数域内存在无法整除的情况，因此需要将运算限定在伽罗华域内进行。

构造

本原多项式 $P(x)$ 是 $GF(2)$ 上的 m 次多项式，具有性质：$(x^{2^m-1}+1)/P(x)$ 的余式为 0，并且 $P(x)$ 不能被 $GF(2)$ 上任意次数小于 m 大于 0 的多项式整除。

举例说明 $GF(2^3)$ 构造方法，选择本原多项式 $P(x)=x^3+x+1$ ，令 $P(x)=0$ 的根为 $\alpha$ ，即 $\alpha^{3}+\alpha +1=0$，伽罗华域加法运算为异或，所以 $\alpha^{3}= \alpha+1$。利用本原元 $\alpha$ 的幂次可以生成该域下所有的元素(除 0 外)，如下表：

如果 $(x^{n}+1)$ 能整除 $P(x)$ 【次数为 $m$ 】，其最小次数(正整数) $n=2^m-1$ ，所以有 $\alpha^{2^m-1}=1=\alpha^0$ ，即幂次达到 $n=2^m-1$ 重新回到 $\alpha^0$ 即等于 1，所以扩域 $GF(2^w)$ 共有 $2^w$ 个元素(包括元素0).

2. 矩阵

Vandermonde 矩阵

实数域
$m \times n$ 的 Vandermonde 矩阵形式如下，$V_{ij}=\alpha^{j-1}$，（常见取 $x_1,x_2,\cdots,x_m$ 为 $1,2,\cdots,m$）

$\begin{bmatrix} 1 & \alpha_1 & \alpha_1^2 & \cdots & \alpha_1^{n-1} \\ 1 & \alpha_2 & \alpha_2^2 & \cdots & \alpha_2^{n-1} \\ 1 & \alpha_3 & \alpha_3^2 & \cdots & \alpha_3^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \alpha_m & \alpha_m^2 & \cdots & \alpha_m^{n-1} \end{bmatrix}$

实数下的不同元素的 Vandermonde 矩阵 $(n \times n)$ 是一定可逆的，但它的任意 m 行 m 列(m<n)组成的子矩阵不一定是可逆的.

【参考mathoverflow】

1. 对于实数下的 vandermonde 矩阵，元素为 不同正数时 任意的子方阵是可逆的(*)
2. 由于 $n*n$ 的 Vandermonde 方阵是可逆的，若 $m>n$ 则任意的 $n*n$ 的子方阵是可逆（也是范德蒙矩阵）【可逆证明提示：n 次多项式最多有 n 个根；其行列式不等于0】

【实数域下的可逆性】

互不相等的实数构成的范德蒙矩阵是可逆的，这里考虑它的任意子方阵。

【有限域下的可逆性】

实数域下可能不可逆，有限域下更可能如此。

注意： 根据【Note: Correction to the 1997 Tutorial on Reed-Solomon Coding】来构造 VRS 的生成矩阵。

Cauthy 矩阵

$m \times n$ 的 Cauthy 矩阵形式如下：

• $X=\{ x_1,x_2,\dots , x_m\}$，$Y=\{ y_1,y_2,\dots , y_n\}$，【都是 $GF(2^w)$ 元素】
• 满足 $X \cap Y = \emptyset$，即任意 $x_i \neq y_j,x_i \neq x_j, y_i \neq y_j$ (都不相同)

$\begin{bmatrix} \frac{1}{x_1+y_1} & \frac{1}{x_1+y_2} & \frac{1}{x_1+y_3} & \cdots & \frac{1}{x_1+y_n} \\ \frac{1}{x_2+y_1} & \frac{1}{x_2+y_2} & \frac{1}{x_2+y_3} & \cdots & \frac{1}{x_2+y_n} \\ \frac{1}{x_3+y_1} & \frac{1}{x_3+y_2} & \frac{1}{x_3+y_3} & \cdots & \frac{1}{x_3+y_n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{1}{x_m+y_1} & \frac{1}{x_m+y_2} & \frac{1}{x_m+y_3} & \cdots & \frac{1}{x_m+y_n} \end{bmatrix}$

对应的行列式的值为证明：

$D_n=\frac{\prod\limits_{1\leq i \leq j \leq n} (a_j-a_i)(b_j-b_i)}{\prod\limits_{i=1}^{n} \prod\limits_{j=1}^{n} (a_i+b_j)}$

Cauchy 矩阵的任意 n 行 n 列组成的矩阵都是可逆的, 因为任意子矩阵还是 Cauchy 矩阵.

【实数域下的可逆性】

在上述条件下，Cauthy 矩阵是非奇异矩阵，可逆矩阵。

【有限域下的可逆性】

矩阵也是非奇异矩阵

矩阵编码

• 利用单位矩阵扩展 Vandermonde 后的 $n \times k$ 矩阵，可能任意 $k$ 行的子矩阵不可逆，在有限域中也是如此。
• 通常使用 Vandermonde 矩阵，做矩阵的初等变换使得前 $k \times k$ 是单位矩阵。
• 可以直接使用单位矩阵扩展 Cauthy 矩阵，任意的子方阵仍然可逆。

Cauchy Reed-Solomon 的优化

使用 Cauthy 矩阵

可逆性更好，构造更加简单；可以在 $O(n^2)$ 完成矩阵的逆运算

投影到 $GF(2)$

方法：每个 $GF(2^w)$ 中的元素 $e$ 可以表示为一个 $w$ 维的列向量 $V(e)$（多项式系数或二进制表示）；每个元素 $e$ 同样可以表示为一个 $w \times w$ 的二进制矩阵 $M(e)$，其第 $i$ 列是 $e*2^{i-1}$ 的二进制表示即 $V(e*2^{i-1})$。例如在 $GF(2^3)$ 下元素的表示为：

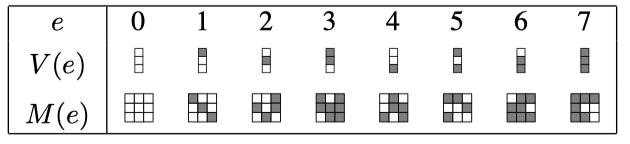
得到结论：

1. 根据映射关系，不同元素对应的 $M(e)$ 是不同的
2. 基于标准的位运算 $M(e_1) * V(e_2) = V(e_1e_2)$
3. 基于标准的位运算 $M(e_1) * M(e_2)=M(e_1e_2)$

根据结论，可以将 $GF(2^w)$ 的运算转化为 $GF(2)$ 下标准的位运算（异或，按位与），降低了运算的复杂度。

(2)的理解

用 $e_{i,j}$ 表示元素 $e_i$ 二进制的第 $j$ 位：

$\begin{aligned} e_1e_2 &= e_1(e_{2,0}2^{0}+e_{2,1}2^{1}+\dots+e_{2,w-1}2^{w-1}) \\ &= e_12^0*e_{2,0}+e_12^1*e_{2,1}+ \dots +e_12^{w-1}*e_{2,w-1} \\ &= \begin{bmatrix} e_12^0 & e_12^1 & \cdots & e_12^{w-1}\end{bmatrix} \cdot \begin{bmatrix} e_{2,0} \\ e_{2,1} \\ \vdots \\ e_{2,w-1} \end{bmatrix} \end{aligned}$

将对应的元素映射为 $w$ 向量，即可：

$V(e_1e_2)=M(e_1) * V(e_2)$

(3)的理解

$\begin{aligned} M(e_1)*M(e_2) &= M(e_1) \cdot \begin{bmatrix} V(e_22^0) & V(e_22^1) & \cdots & V(e_22^{w-1}) \end{bmatrix} \\ &= \begin{bmatrix} V(e_1e_22^0) & V(e_1e_22^1) & \cdots & V(e_1e_22^{w-1}) \end{bmatrix} \\ &= M(e_1e_2) \end{aligned}$

链接

工具

1. 有限域的计算工具
2. 快速乘法

问答

1. Linear independence of Vandermonde matrix in systematic Reed-Solomon code

论文

1. A Tutorial on Reed-Solomon Coding for Fault-Tolerance in RAID-like Systems
2. Note: Correction to the 1997 Tutorial on Reed-Solomon Coding
3. Optimizing Cauchy Reed-Solomon Codes for Fault-Tolerant Storage Applications
4. An XOR-Based Erasure-Resilient Coding Scheme
5. Tutorial: Erasure Coding for Storage Applications