信息论基础

熵 Entropy 的定义

离散型随机变量 $X$ (字母表为 $\mathcal{X}$，概率函数 $p(x) = Pr(X=x), x\in \mathcal{X}$)，entropy 熵定义为：

$H(X) = - \sum\limits_{x\in \mathcal{X}} p(x)\log p(x) = -E\log p(x)$

• $0\log 0 \rightarrow 0$ ($x$ 趋近于 0，$x\log x$ 趋近于 0 )
• $H(X)\ge 0$
• 当 $X$ 是在 $\mathcal{X}$ 服从均匀分布时，$H(X) = \log |\mathcal{X}|$
• $H_b(X)= \log_{b}a H_a(X)$ - 算法/定义中的对数如果以 $b$ 为底，熵记作 $H_b(X)$ - 以 2 为底，单位为 bits - 以自然常数 e 为底，单位为 nats
  （衡量信息量大小，不确定性大小）

例子

二进制熵函数

$\text{Let }X = \begin{cases} 1 & \text{with probablity }p\\ x & \text{with probability }1-p \end{cases}$

系统的熵： $H(x)=-p\log p - (1-p)\log(1-p)$ ，关系如下：

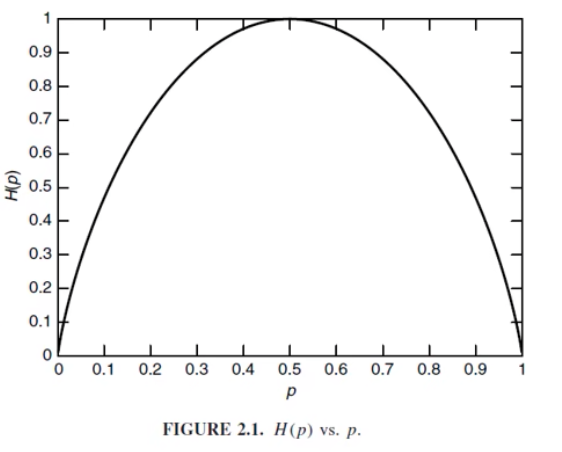
性质

说明：

• 凹函数(凹向下)的性质 ^[1]
• 这里的 $\lambda_{1},\lambda_{2},\cdots$ 取值都是 $\frac{1}{|\mathcal{X}|}$
• 当且仅当，均匀分布取到最大熵 (均匀分布最大化离散熵)

根据熵的定义，它只由概率分布确定，根据概率分布，可以得到联合熵、条件熵，链式法则。

概率统计中的法则
链式法则：$p(x_1,x_2,\cdots,x_{n)}=p(x_n)p(x_{n-1}|x_{n})\cdots p(x_1|x_2,\cdots,x_{n-1})$
贝叶斯规则：$p(y)p(x|y)=p(x)p(y|x)$

联合熵 Joint Entropy

条件熵 Conditional Entropy

• 条件熵 $H(Y|X)$ 是，在 $p(Y|X=x)$ 上定义的熵，对 x 取加权平均；或者直接根据期望计算。
• 根据期望计算时，使用的是 $p(x,y)$

例子

• 条件熵不可交换变量的位置
• $\boldsymbol{H}(\boldsymbol{X} \mid \boldsymbol{Y})+\boldsymbol{H}(\boldsymbol{Y})=\boldsymbol{H}(\boldsymbol{Y} \mid \boldsymbol{X})+\boldsymbol{H}(\boldsymbol{X})=\boldsymbol{H}(\boldsymbol{X}, \boldsymbol{Y})$
  • 可以根据定义的期望公式证明，参考下面的链式法则
  • 可以从信息的不确定性来理解

链式法则

零熵 Zero Entropy

说明：如果熵 $H(X)=0$ ，对于离散变量 $X$，其概率分布只有一个取值 $Pr(X=x_0)=1$

1. 由 $H(Y|X)=0 \Longrightarrow H(Y|X=x)=0$ ，根据它的定义容易得到；
2. 由 $H(Y|X=x)=0$，容易知道 Y 在 $X=x$ 下只有一个确定的取值；
3. Y 是 X 的函数。

相对熵 Relative Entropy

相对熵：用来度量两个概率分布的距离

相对熵 (Kullback-Leibler(KL)距离) ，在字母表 $\mathcal{X}$ 上的两个概率分布函数 $p(x),q(x)$ 的 KL 距离定义为：

$\begin{aligned} D(p \| q)= & \sum_{x \in X} p(x) \log \frac{p(x)}{q(x)} \\ & =E_p \log \frac{p(X)}{q(X)} \end{aligned}$

说明：

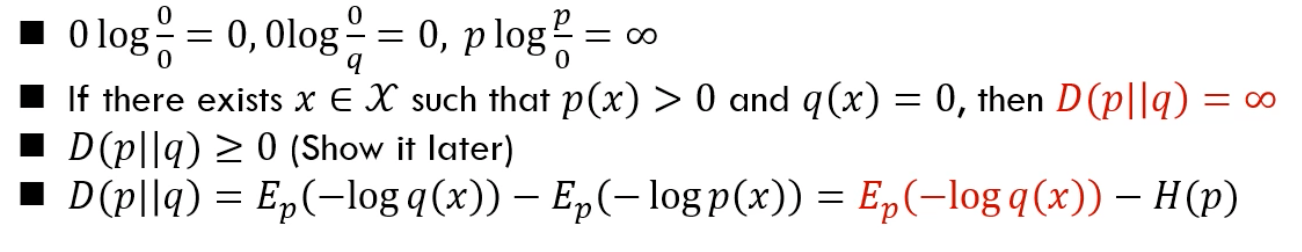
Not Metric

相对熵不是一种 Metric 测度

互信息 Mutual Information

互信息，用来衡量两个随机变量的关联程度（相互拥有的信息量），使用相对熵【p(x,y) 与 p(x)p(y)】来定义：

• 互信息的两个变量可以交换位置
• 两个相互独立的互信息为 0；同一个变量的互信息为它的熵
• 互信息 $I(X;Y)$ 中，使用分号 ; 分隔两个变量

Venn 图

使用 Venn 图理解多个信息量的度量

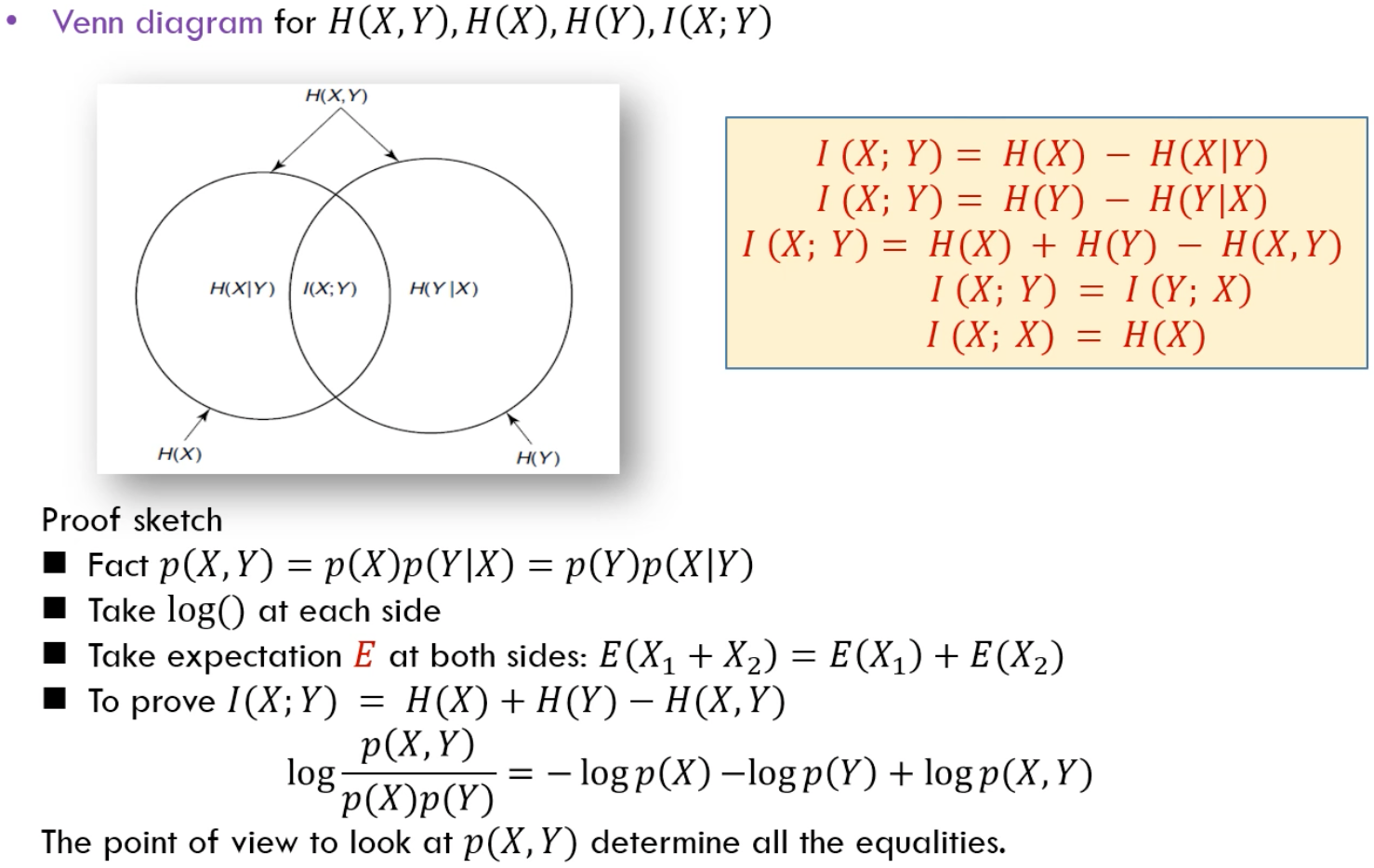
多个变量的链式法则

条件互信息

为了描述在变量 $Z$ 给定条件下，变量 $X,Y$ 的互信息量(符号中 $\mid Z$ 是整体，表示条件 $Z$)

条件相对熵

条件相对熵和相对熵的链式法则：

链接

• 中山大学教学资料
• 信息论基础中文版-Cover
  • 英文版-Cover
• An Introduction to Single-User Information Theory.pdf