Simple Regenerating Codes: Network Coding for Cloud Storage

简单再生码，能够以较低成本简单快速地精确修复，编码效率接近$\frac{2}{3}$

Ⅰ. INTRODUCTION

编码的分布式存储系统中一个中心问题是在故障发生时保持系统编码表示，即维持系统的冗余。

网络编码：修复纠删码系统中的节点故障需要编码分组(coded packets)的网络内(in-network)组合。

在研究精确修复问题中，有几个指标可以优化：修复期间从现有磁盘读取的总信息量、网络中通信的总信息量（修复带宽）或每次修复所需访问的磁盘总数。

Ⅱ. SIMPLE REGENERATING CODES

A. 编码构造

将文件 $\mathbf{f}$，大小为 $M=2k$，划分为 2 部分 $\mathbf{f}=[\mathbf{f^{(1)}}\ \mathbf{f^{2}}],\ \mathbf{f}^{(i)} \in \mathbb{F}^{1 \times k},\ i \in [1,2]$。编码过程分为两步：

1. 编码过程

通过一个 $(n,k)$ 的 MDS 编码将文件的两个部分（即 $\mathbf{f^{(1)}}\ \mathbf{f^{2}}$）分别编码（因为每一个部分都有 $k$ 个符号），记编码后编码块分别为长度为 $n$ 的向量 $\mathbf{x}$ 和 $\mathbf{y}$：

$\mathbf{x}=\mathbf{f}^{(1)}\mathbf{G} \\ \mathbf{y}=\mathbf{f}^{(2)}\mathbf{G} \tag{1}$

其中 $\mathbf{G} \in \mathbb{F}^{k\times n}$ 是 $(n,k)$ MDS 码生成矩阵，其最大距离性质保证了任意 $\mathbf{x}$ 或 $\mathbf{y}$ 的 $k$ 个编码块都可以分别重建 $\mathbf{f^{(1)}}$ 或 $\mathbf{f^{2}}$；最后通过异或生成 $\mathbf{s}$ :

$\mathbf{s}=\mathbf{x}+\mathbf{y} \tag{2}$

上述的编码过程一共产生 $2n+n=3n$ 个编码块（符号）。

2. 块放置策略

目的：将 $3n$ 个编码块放置到 $n$ 个节点，则每个节点存储 3 个编码块。
方法：每个节点分别存储来自 $\mathbf{x},\mathbf{y},\mathbf{s}$ 的一个编码块，要求 3 个编码块下标都互不相同。对于 $n \geq 2$ 都可以采用如下的循环放置来实现：

B. 纠删弹性和码率

可以容忍任意的 $n-k$ 个故障，从两个分别的 MDS 编码过程得到。

$(n,k)-SRC$的编码效率(space efficiency) $R$ 等于有用的存储信息总量与存储数据总量之比：

$R=\frac{file \ size}{storage \ spent}=\frac{2 \cdot k}{3 \cdot n} \tag{3}$

并且上界是 $\frac{2}{3}$，$m$ 固定时，$R=\frac{2}{3}\frac{k}{k+m} \stackrel{k \rightarrow \infty}{\longrightarrow} \frac{2}{3}$。

C. 修复丢失块

由于丢失的每个块与存储在 2 个节点中的另外 2 个编码块为同一个索引，因此 SRC 能够轻松修复单个丢失的编码块或单个节点故障，通过通信这两个存活节点，可以通过简单的异或操作修复丢失的块。

修复单节点故障需要 2 倍丢失数据（6 个块）的修复带宽和磁盘读取，需要访问 $d=\min{(n-1,4)}$ 个磁盘。

(4,2)-SRC 举例

举例 $(n=4,k=2)-SRC$，原始的数据对象划分为 $f_1,f_2,f_3,f_4$，分为 2 组，将 $[f_1 \ f_2]$ 编码成 $[x_1 \ x_2 \ x_3 \ x_4]$；将 $[f_3 \ f_4]$ 编码成 $[y_1 \ y_2 \ y_3 \ y_4]$，最后通过异或得到 $[s_1 \ s_2 \ s_3 \ s_4]$，过程如下：

Ⅲ. SIMULATIONS

使用云存储模拟器将所提出 $SRC$ 码与 Replication 和 Reed-Solomon 码进行了比较。

主要的实验分析：

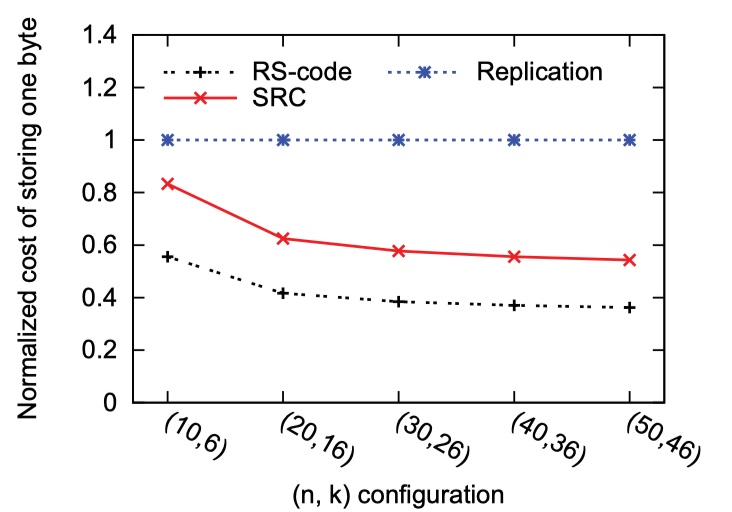
存储开销分析

$n-k=4$ 的存储开销对比：

修复性能

测量修复故障节点时的吞吐量

• 3-副本的修复性能最好，其次是 SRC，而 RS 码的修复性能最差。（考虑修复需要访问的数据量）
• 在不同的 $(n,k)$ 下，SRC 的修复性能保持不变，但随着 n 的增加，RS 码的修复性能变差；其主要优点之一：修复性能独立于 $(n,k)$。
• 此外，SRC 的修复吞吐量约为 500MB/s，约为 3-副本性能的 64%。

数据可靠性分析

使用一个简单的马尔可夫模型[3]来估计可靠性。为简单起见，故障仅发生在磁盘上，假定故障没有相关性。

• SRCs 的可靠性远远高于 3-副本（$10^9$）。即使对于高码率(50，46)，SRC 也比 3-副本可靠几个数量级。受益于 SRC 的高修复速度。
• RS 码呈现明显不同趋势。虽然(10，6)和(20，16)的可靠性高于 3-副本，但随着(n，k)的增长，RS 码的可靠性大大降低。因为它们的修复性能随着 k 的增加而迅速下降。

Ⅳ. CONCLUSIONS

1. 提出了结构简单的 SRC，主要特点：

• $(n,k)-SRC$ 可以容许任意 $n-k$ 个节点故障，是 MDS 编码；
• 码率（编码效率）为 $\frac{2k}{3n}$ ，可以无限接近 $\frac{2}{3}(k \rightarrow \infty)$
• 修复单个节点很高效，得益于特定的块放置策略和编码过程中第二步的异或编码，可以实现精确修复；修复单个节点最多访问 $\min\{n-1, 4\}$ 个磁盘（节点），修复带宽和访问的数据量都是丢失数据的2倍。
• 总体上是一个结构简单，易于实现的一类编码。

2. 主要思想：两个 MDS 预编码用于针对任何 $n-k=m$ 故障提供可靠性，而应用于 MDS 编码分组之上的 XOR 在单节点故障发生时提供有效精确修复。

附录（折衷）

上述将文件 $\mathbf{f}$，大小为 $M=2k$，划分为 2 部分。一般 $(n,k,f)-SRC$，将数据分为 $M=fk$，划分为 $f$ 个部分，编码策略一样，共生成 $(f+1)n$ 个编码块，每个节点存储 $f+1$ 个块。分析：

• 编码效率($R$)

$R_{SRC}=\frac{file \ size}{storage \ spent}=\frac{f \cdot k}{(f+1)\cdot n}$

编码效率是 $(n,k)$ MDS 码的 $\frac{f}{f+1}$

• 每个节点的存储($\alpha$)

$\alpha_{SRC}=\frac{f+1}{f} \cdot \frac{M}{k}$

• 单个节点的修复带宽($\gamma$)

$\gamma_{SRC}=f(f+1)=(f+1)\frac{M}{k}$

• 单节点修复的磁盘访问个数($d$)

$d_{SRC}=\min(n-1, 2f)$

参考论文

1. A. G. Dimakis, P. G. Godfrey, Y. Wu, M. J. Wainwright, and K. Ramchandran, “Network coding for distributed storage systems,” in IEEE Trans. on Inform. Theory, vol. 56, pp. 4539 – 4551, Sep. 2010.
2. A. G. Dimakis, K. Ramchandran, Y. Wu, and C. Suh, “A survey on network codes for distributed storage,” in IEEE Proceedings, vol. 99, pp. 476 – 489, Mar. 2011.
3. D. Ford, F. Labelle, F. I. Popovici, M. Stokely, V.-A. T. L. Barroso, C. Grimes, and S. Quinlan, “Availability in globally distributed storage systems,” in OSDI ’10: Proc. of the 9th Usenix Symposium on Operating Systems Design and Implementation, 2010.