Leetcode
Leetcode 算法题分析
数组和字符串
Leetcode 189. 轮转数组
给定一个整数数组
nums,将数组中的元素向右轮转k个位置,其中k是非负数。
解法 1,利用多次翻转实现
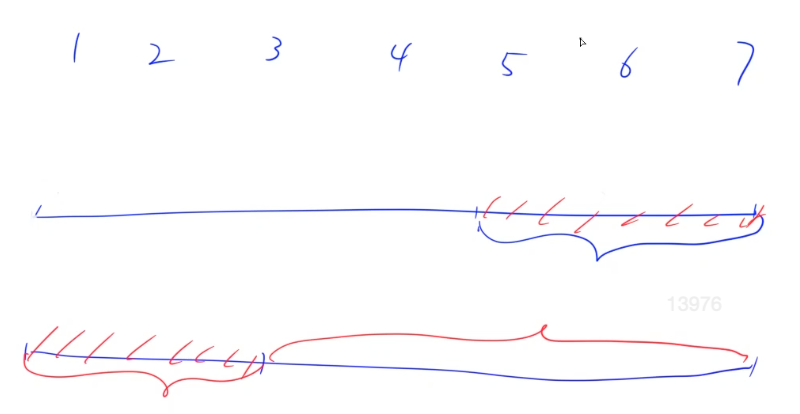
容易理解的做法。使用一个具体数组进行模拟,关注最后 个元素的位置移动后的位置,利用数组翻转来改变元素的位置关系。
- 先将所有元素翻转,这样尾部的 个元素就被移至数组头部
- 然后再翻转区间 和区间 即可
Code示例
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k = k%n;
// 翻转一次
for(int i=0, j=n-1; i<j; i++, j--)
swap(nums[i], nums[j]);
// 再次翻转,调整局部顺序
for(int i=0, j=k-1; i<j; i++, j--)
swap(nums[i], nums[j]);
for(int i=k, j=n-1; i<j; i++, j--)
swap(nums[i], nums[j]);
}
};
解法 2,环形替换
将每个数字放至它最后的位置,为了避免放置位置的元素被覆盖,使用临时变量 来保存。例如从位置 0 开始,最初令 。根据规则,位置 0 的元素会放至 的位置,令 ,此时交换 和 ,完成位置 j 的更新。然后,我们考察位置 j,并交换 temp 和 ,从而完成下一个位置的更新。不断进行上述过程,直至回到初始位置 0。
注意:一次循环,可能没有遍历完数组中的所有的元素,为了求出需要遍历的次数,需要先考虑这样一个问题:从索引 0 开始不断遍历,最终回到起点 0 的过程中,(即一次循环)遍历了多少个元素?
由于最终回到了起点,该过程恰好走了整数数量的圈,设为 a 圈,再设该过程总共遍历了 b 个元素。因此,得到 ,即 一定是 的公倍数,又因为是第一次回到起点就结束,所有 a 尽可能小,故 就是 的最小公倍数 ,因此
单次遍历只能访问 b 个元素,为了访问到所有元素,因此需要遍历的次数为:
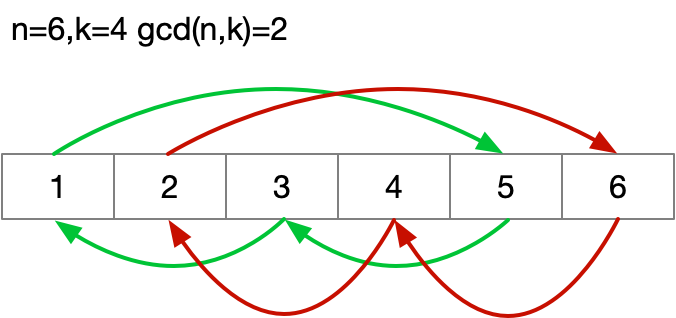
结果就是,需要遍历 最大公约数 次。
以元素 为例,两次遍历的过程为:
Code示例
class Solution {
public:
void rotate(vector<int> &nums, int k) {
int n = nums.size();
k = k % n;
int count = gcd(k, n);
for (int start = 0; start < count; ++start) {
int current = start;
int prev = nums[start];
do {
int next = (current + k) % n;
swap(nums[next], prev);
current = next;
} while (start != current);
}
}
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
};
总结:
- 如果(n,k)互质,从一个初始位置开始,遍历时每次向后移动 k 个位置,可以通过一次循环遍历完整个数组元素。(例如,通过算法生成元素场景中,每次可以生成间隔为 k 的元素,那么最终可以均匀地生成所有 n 个元素)
Leetcode 45. 跳跃游戏 Ⅱ #贪心
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例保证可以到达 nums[n - 1]。
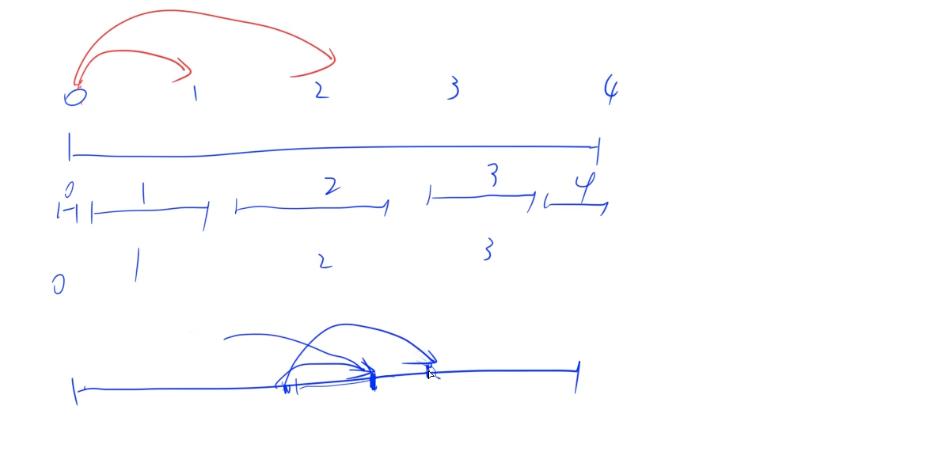
如果用 表示从位置 0 跳到位置 需要的最小跳跃次数,有性质:
- 是分段(连续)递增的,反证法:如果存在相邻 ,有 ,那么存在 可到达 ,因此 达到 最小次数为 ,与假设矛盾。其他情况, 也类似。所以 只能是
在遍历所有元素过程中,根据分段性,更新每一步的最远位置,并记录当前元素需要的最小次数。
Code示例
class Solution {
public:
int jump(vector<int>& nums)
{
int max_far = 0;// 目前能跳到的最远位置
int step = 0; // 跳跃次数
int end = 0; // 跳跃可达范围右边界
for (int i = 0; i < nums.size() - 1; i++)
{
max_far = std::max(max_far, i + nums[i]);
// 到达上次跳跃能到达的右边界了
if (i == end)
{
end = max_far; // 目前能跳到的最远位置变成了下次起跳位置的右边界
step++; // 进入下一次跳跃
}
}
return step;
}
};
代码优化,可以边遍历 的同时,同时找到前一段中位置 可以更新/一步跳到 (其过程类似双指针问题)。
事实: 后面一段(需要 n+1 步走到)的所有位置必定能够在前面一段(需要 n 步)的某个位置 (可能不都是同一个下标)跳一步更新到。
Code示例
class Solution {
public:
int jump(vector<int> &nums) {
int n = nums.size();
vector<int> f(n);
for (int i = 1, j = 0; i < n; i++) {
while (j + nums[j] < i)
j++;
f[i] = f[j] + 1;
}
return f[n - 1];
}
};
Leetcode 134. 加油站 #贪心|#单调队列
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则保证它是唯一的。
解法 1,枚举+贪心优化
思路:先枚举所有的起点,然后每次遍历后续的所有点。优化:如下图所示,假设从起点位置 开始出发,可以行驶到位置 ,但是无法到达下一个位置 ,根据要求发现:
- 如果以中间的位置 作为起点,同样无法到达位置 (即无法转完一圈),反证法。因此如果从 可以到达 ,但是无法到达 ,则下一次起点直接可以从位置 开始。
- 边界,起点位置只位于

Code示例
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int n = gas.size();
for (int i = 0, j; i < n;) { // 枚举起点
int left = 0;
for (j = 0; j < n; j++) { // 枚举当前的终点
int t = (i + j) % n;
left = left + gas[t] - cost[t];
if (left < 0)
break;
}
if (j == n)
return i;
i = i + j + 1; // 跳过
}
return -1;
}
};
解法 2,通用做法,单调队列优化
直接看这一道题:提高课 DP-1088. 旅行问题
思路:将每一个点 的油量与接下来的消耗量的差值 作为该点的值,判断该点顺时针能够回到该点,等价于长度为 的(处理后的数组)所有前缀和 。求解该数组的前缀和数组 后,等价于 ,即固定位置 后,判断其后连续的 个前缀和的最小值 是否满足该条件即可。归结于,求解滑动窗口中的最值问题
总结:
- 如果需要枚举环形上的点,并且长度范围是循环的,可以先展开为线性,做法是将元素复制一遍到末尾;
- 对于逆时针,就是改变求和的方向,等价于固定前缀和窗口的右边界;
Code示例
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
using LL = long long;
const int N = 2e6 + 10;
int n, p[N], d[N];
LL s[N]; // 前缀和
int q[N], hh, tt; // 单调队列
bool st[N]; // 答案数组
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
cin >> p[i] >> d[i];
// 顺时针, 固定左端点,求右窗口中的最小值
for (int i = 1; i <= n; i++)
s[i] = s[i + n] = p[i] - d[i]; // 展开为2*n的数组
for (int i = 1; i <= 2 * n; i++)
s[i] += s[i - 1]; // 前缀和
hh = 0, tt = -1;
for (int i = 2 * n; i; i--) { // 从左往右也可以
if (hh <= tt && q[hh] - i >= n)
hh++;
while (hh <= tt && s[i] <= s[q[tt]])
tt--;
q[++tt] = i; // 添加i共n个
if (i <= n && s[q[hh]] >= s[i - 1])
st[i] = true;
}
// 逆时针, 固定右端点,求左窗口中的最大值
d[0] = d[n];
for (int i = 1; i <= n; i++)
s[i] = s[i + n] = p[i] - d[i - 1];
for (int i = 1; i <= 2 * n; i++)
s[i] += s[i - 1];
hh = 0, tt = -1;
for (int i = 1; i <= 2 * n; i++) {
// 注意未加入i之前,窗口最多有n个值
if (hh <= tt && i - q[hh] > n)
hh++;
// 当 i=[n+1...2n] 判断结果
// 这里需要判断 a[i],先判断后加入i
if (i > n && s[i] >= s[q[hh]])
st[i - n] = true;
while (hh <= tt && s[i] >= s[q[tt]])
tt--;
q[++tt] = i;
}
for (int i = 1; i <= n; i++)
if (st[i])
cout << "TAK" << endl;
else
cout << "NIE" << endl;
}
链表
排序:
- Leetcode 148. 排序链表 链表的归并排序,从底向上写法。代码示例
二叉树/树
遍历
- Leetcode 144. 二叉树前序遍历 二叉树前序遍历迭代写法。代码示例
- Leetcode 94. 二叉树中序遍历 二叉树中序遍历迭代写法。代码示例
- Leetcode 145. 二叉树后序遍历 二叉树后序遍历迭代写法。代码示例 思路 1 使用常规方法和标志位,思路 2 转化为前序遍历方式。
- Leetcode 102. 二叉树的层序遍历 使用队列广度优先遍历。代码示例
对于递归改迭代,具有机械化的改法,例如中序遍历,添加节点的状态来辅助遍历:https://www.acwing.com/solution/content/176/
使用遍历的扩展题目
- Leetcode 513. 找树左下角的值 深度优先遍历/广度优先遍历
序列化
- Leetcode 652. 寻找重复的子树 二叉树自定义唯一值序列化。代码示例
动态规划
数字三角形 DP
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
对动态规划中空间优化的总结:
- 如果可以使用滚动数组来优化存储空间时,使用
row & 1来确定当前行位置(利用 2 行的数组进行滚动计算),其中&运算符优先级低于+, - - 算法题中,可以先使用常规二维数组进行解题和计算,最后将原状态数组改成 2 行的滚动数组,并机械化地将使用到的状态行 row 全部用
row & 1替换即可
Code示例
class Solution {
public:
//* 这里倒序计算,可以直接使用一维数组
// vector<int> getRow(int rowIndex) {
// // 倒序不会覆盖元素
// vector<int> f(rowIndex + 1);
// for (int i = 0; i <= rowIndex; i++) {
// f[0] = f[i] = 1;
// for (int j = i - 1; j > 0; j--)
// f[j] = f[j - 1] + f[j];
// }
// return f;
// }
//* 一般的滚动数组优化方法
vector<int> getRow(int rowIndex) {
vector < vector >> f(2, vector<int>(rowIndex + 1));
for (int i = 0; i <= rowIndex; i++) {
f[i & 1][0] = f[i & 1][i] = 1;
for (int j = 1; j < i; j++)
f[i & 1][j] = f[i - 1 & 1][j - 1] + f[i - 1 & 1][j];
}
return f[rowIndex & 1];
}
};
字符串匹配
实现一个函数用来匹配包括'.'和'*'的正则表达式。
DP 分析:
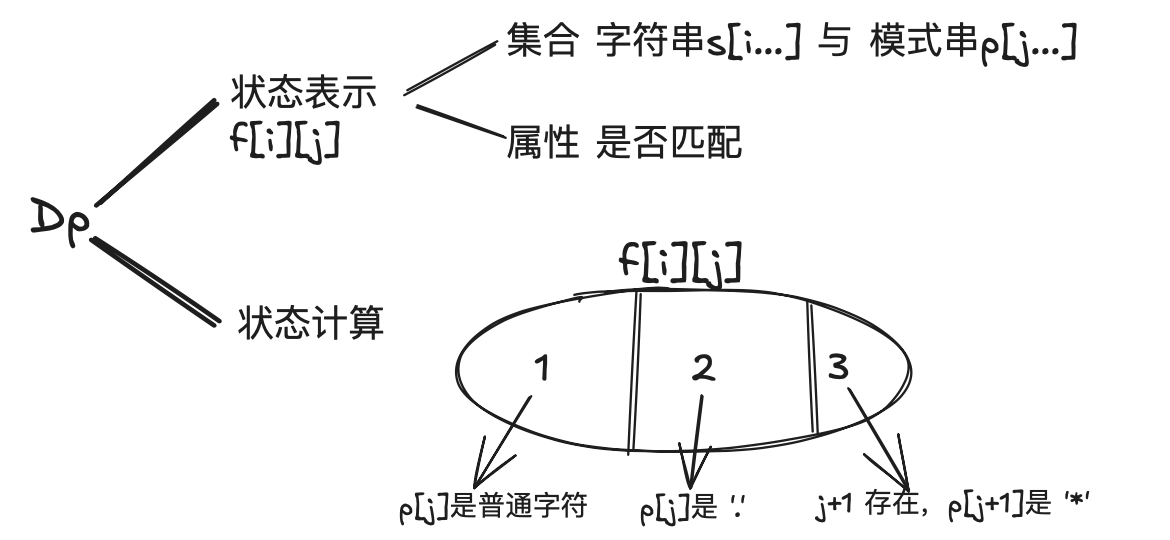
注意,在状态计算中,第3种情况其实是 1/2 中的子分类,但是单独拿出来进行计算可以减少分类讨论情形。结果只需要计算出是否匹配,分类能完全覆盖 f[i][j] 的状态即可。
class Solution {
// f[i][j] 表示 s[i...] 与 p[j...] 的匹配状态
vector<vector<bool>> f;
public:
bool isMatch(string s, string p) {
int n = s.size(), m = p.size();
f=vector<vector<bool>>(n+1, vector<bool>(m+1, false));
f[n][m] = true;
// f[n][j] 需要计算
for(int i=n; i>=0; i--){
for(int j=m-1; j>=0; j--){
// i<n 排除 s 是空串的情况,避免出现访问 s[i]/f[i][j]越界
bool first_match = i<n && (s[i] == p[j] || p[j] == '.');
f[i][j] = first_match && f[i+1][j+1]; // 不考虑 *
// 考虑 *
if(j+1<m && p[j+1]=='*'){
f[i][j] = f[i][j+2] || (first_match && f[i+1][j]); // 0 次 || 至少1次
}
}
}
return f[0][0];
}
};
/**
* 写法2
* 递归形式计算 f[0][0] 并计算状态
*/
class Solution {
// f[i][j] 表示 s[i...] 与 p[j...] 的匹配状态
vector<vector<int>> f; // int: 单独使用 -1 表示还未计算
string s, p;
int n, m;
public:
bool isMatch(string _s, string _p) {
s = _s, p = _p;
n = s.size(), m = p.size();
f=vector<vector<int>>(n+1, vector<int>(m+1, -1));
return dp(0, 0);
}
bool dp(int i, int j){
if(f[i][j]!=-1) return f[i][j];
if(j == m)
return f[i][j] = i ==n;
bool first_match = i<n && (s[i]==p[j] || p[j] == '.');
f[i][j] = first_match && dp(i+1, j+1);
if(j+1<m && p[j+1] == '*')
f[i][j] = dp(i, j+2) || (first_match && dp(i+1, j));
return f[i][j];
}
};
类似的题目:
本文链接: Leetcode
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。
发布日期: 2024-05-19
最新构建: 2025-05-16
欢迎任何与文章内容相关并保持尊重的评论😊 !