Jerasure-1.2

说明: 对Jerasure-1.2版本重点接口和编码的理解和梳理，2.0版本类似。主要参考此版本的说明手册和源代码，可以再 这里 找到相关资料。

相关资料见 参考链接

原理分析

使用 schedule 代替 bit-matrix

参考Jerasure1.2手册$4.1；将稀疏位矩阵中的 1 用 5元组 来表示，通过确定的多个 5 元组表达式运算完成编码块共 $m \times w$ 个 packets 的编码计算。

notes: 编码时，数据元素和编码元素为二进制形式，数据块和编码块都分成了 w 个 packet，每次对 packet 的元素进行并行操作【 $M(e_1)*V(e_2)=V(e_1e_2)$ 】。

代码分析

对 Cauthy 矩阵位矩阵的 计划表优化 做了分析。

回顾一下位矩阵的解码过程，与经典的 RS 等解码类似

下图使用生成矩阵｜分布矩阵生成校验块的过程，省略了数据块部分：

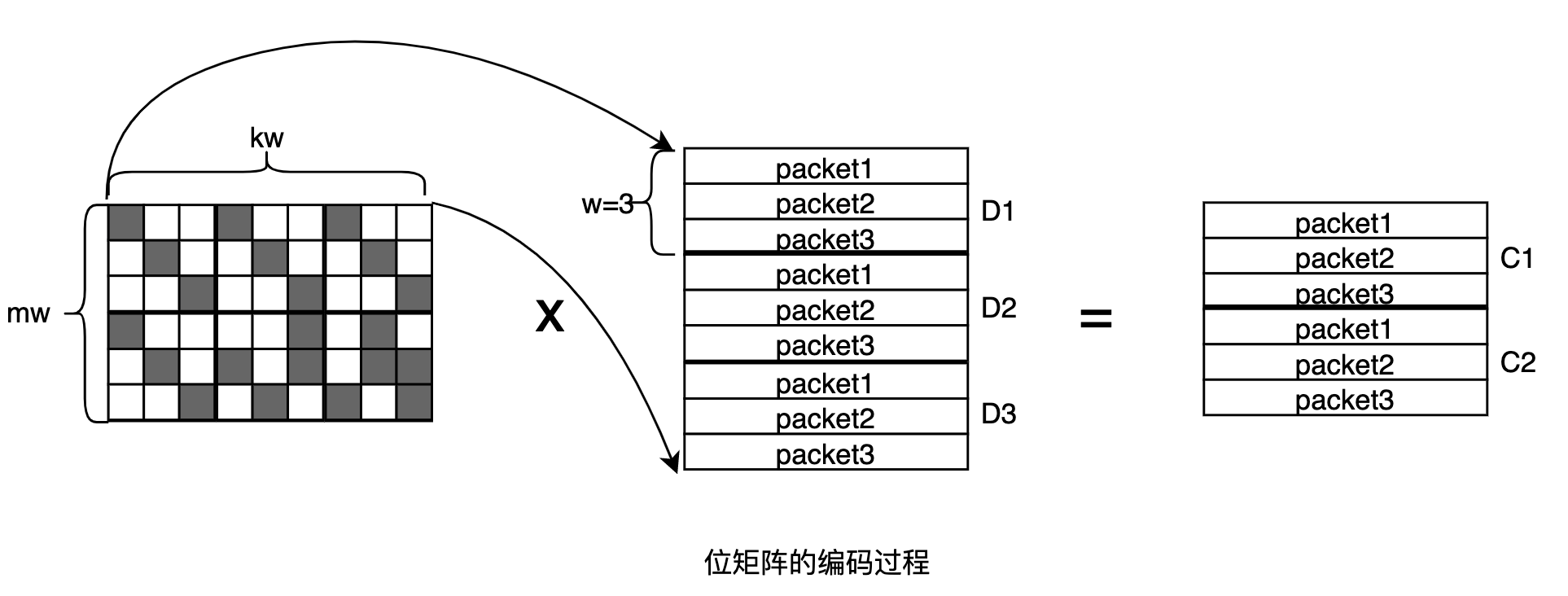
假设 D 1、C 1 失效，选取前 k 个没有失效的编码块对应的超行作为新的分布矩阵，其逆矩阵通常称作为解码矩阵 decoding matrix：

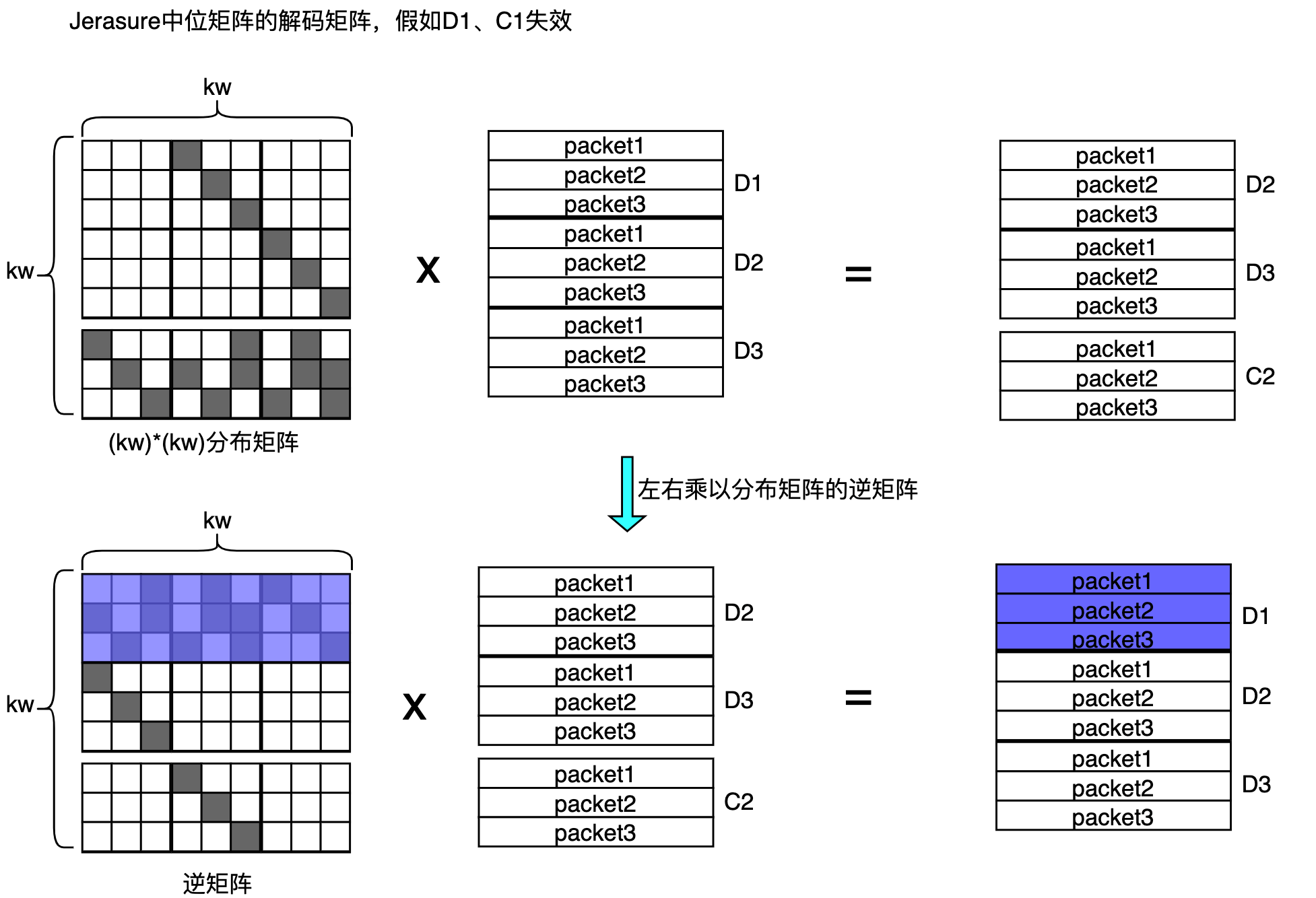
说明：

• Jerasure 中选取的 $(kw) \times (kw)$ 的分布式矩阵的 编码块对应的超行(w行) 顺序为 C2、D2、D3 对应的超行。前 k 个中失效的数据块用未失效的校验块替代，而将失效的数据块和失效的校验块放在 k 之后用于计划表的操作。这种方式能够同时解码出失效的检验块。
• 通常使用上图的逆矩阵的部分超行来解码出数据块，再重新编码恢复校验块也可以。

Jerasure 使用位矩阵生成计划表过程中的完整解码矩阵的构造：主要来自函数 erasure_generate_decoding_schedule

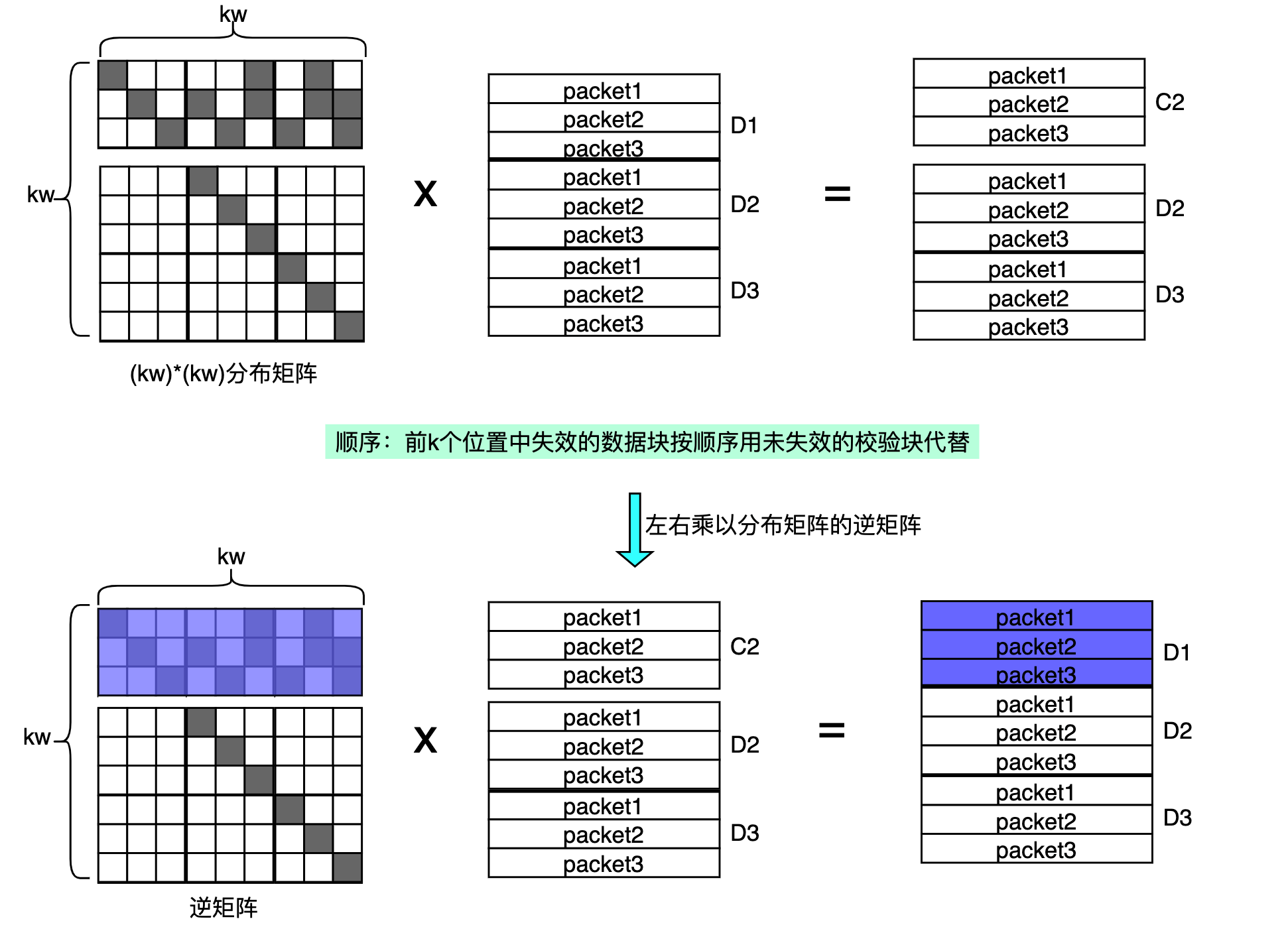
最后完整的解码矩阵由两部分构成，用于恢复数据块的超行，和用于恢复校验块的超行：

1. 根据图中最后一步，选择失效的数据块对应的逆矩阵的超行，作为解码矩阵的第一部分；
2. 第二部分由编码矩阵(生成矩阵)中失效块对应的超行运算得到：

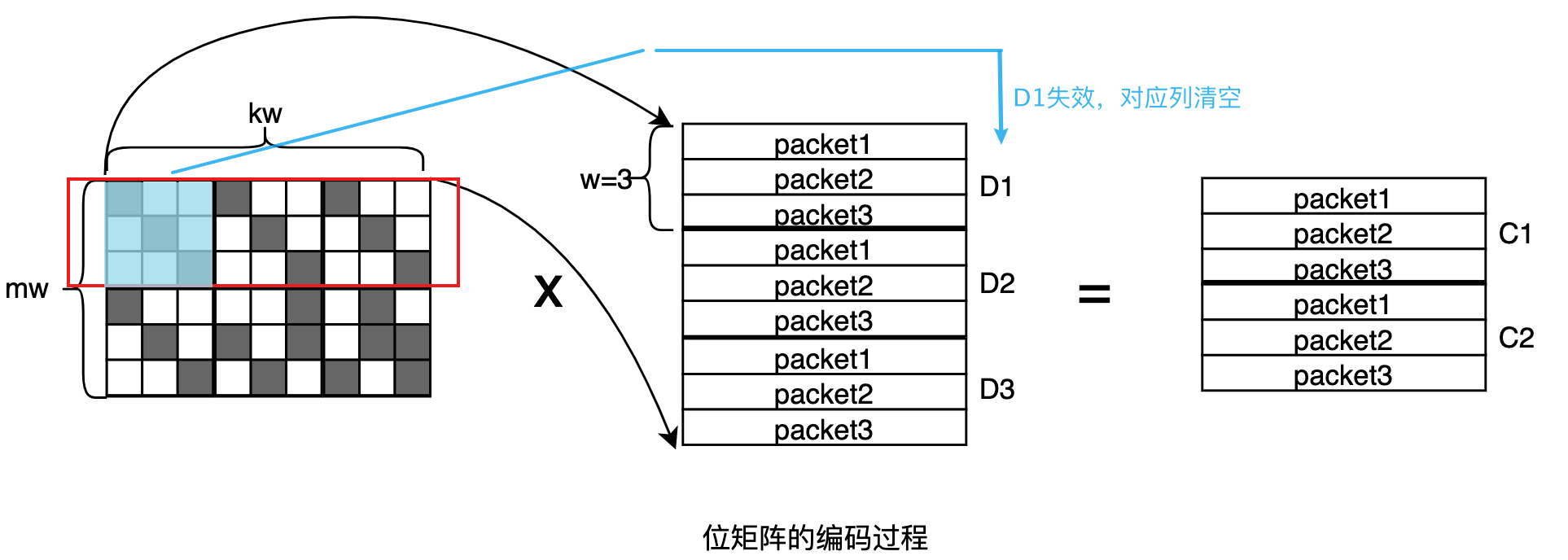
(1) 先复制编码矩阵中的对应的超行到最终的解码矩阵，将失效数据块对应的列置为 0

(2) 遍历编码矩阵的置为0的列(即置0的位置)的位置 $i \in [0,w)$，如果为 1，解码矩阵的该行异或逆矩阵或者最终编码矩阵解出数据块超行的第 i 行。

说明：如果没有数据块失效，则直接复制解码矩阵中，与编码过程一样。Jerasure 中的解码都是通用的解码方法，将失效的数据块和失效的校验块都修复好。

例如：第一步后，

0 0 0 | 1 0 0 | 1 0 0  ==> (2)只需要异或蓝色超行中第0行(只有一个1)
0 0 0 | 0 1 0 | 0 1 0  ==> (2)只需要异或上图紫色超行中第1行
0 0 0 | 0 0 1 | 0 0 1  ==> (2)只需要异或上图紫色超行中第2行

经过第二步后：

1 0 0 | 1 0 1 | 1 1 0
0 1 0 | 1 1 1 | 0 0 1
0 0 1 | 0 1 1 | 1 0 0

可以得到 C 1 的 3 个 packets 表达式：

$p_1 = C_2p_1 \oplus D_2p_1 \oplus D_2p_3 \oplus D_3p_1 \oplus D_3p_2 \\ p_2 = C_2p_2 \oplus D_2p_1 \oplus D_2p_2 \oplus D_2p_3 \oplus D_3p_3 \\ p_3 = C_2p_3 \oplus D_2p_2 \oplus D_2p_3 \oplus D_3p_1$

将 C 2 替换掉：

$p_1 = D_1p_1 \oplus D_2p_1 \oplus D_3p_1 \\ p_2 = D_1p_2 \oplus D_2p_2 \oplus D_3p_2 \\ p_3 = D_1p_3 \oplus D_2p_3 \oplus D_3p_3$

由此可以看出，恢复校验块的策略是对的。证明思路：由于完整的解码矩阵相乘的编码块与 编码的k个数据块 有区别，我们取超行中的一行 1*(kw)来看，记作 $b=(b_1\ b_2…b_k)$ ，则根据编码得到该超行编码块中的第 $i$ 个 packet 为

$p_i = (b1\ b_2...b_k) \cdot [p^1\ p^2 ... p^k]^T$

假如第一个数据块失效，将对应的 packets 用解码矩阵中的超行与幸存的前 k 个编码块点积代替。记幸存的前 $k$ 个编码块为 $p^c,p^2…p^k$ ，即 $C_1,D_2…D_k$ ；$a_i$ 是用到的失效数据块再解码解码矩阵的超行中的第 $i$ 行：

$p_i = (b1\ b_2...b_k) \cdot [(a_1(p^c,p^2...p^k) \dots a_w(p^c,p^2...p^k));...;p^k]^T \\ =b_{11}a_1(p^c,p^2...p^k)+...+b_{1w}a_w(p^c,p^2...p^k)+ \\ b_2p^2+b_3p^3+...+b_kp^k \\ =(b_{11}a_1+...+b_{1w}a_w)p^c+(b_{11}a_1+...+b_{1w}a_w+b_2)p^2+...+(b_{11}a_1+...+b_{1w}a_w+b_k)p^k$

很容易得出结论。

::: danger 说明

上述过程是将修复数据块和校验块同时修复，来构造完整的解码矩阵，主要目的是生成统一的计划表(都是对同样的 $k$ 个编码块的 $kw$ 个 $packets$ 做操作)

:::

使用与测试

主要供上层调用的 接口函数，是 MDS 编码的接口；部分源代码和注释在线阅读参考

编码

• 常规有限域内的编码函数

  jerasure_matrix_encode(int k, int m, int w, int matrix, char **data_ptrs, char **coding_ptrs, int size)

• 二进制矩阵下编码函数

  jerasure_bitmatrix_encode(int k, int m, int w, int *bitmatrix, char **data_ptrs, char **coding_ptrs, int size, int packetsize)

  ---

• 使用位矩阵转换得到的 schedule 的编码函数（效率比直接使用二进制矩阵高，需要自己先调用 dumb 或 smart 两个计划表生成函数将位矩阵（通常是编码矩阵和解码矩阵）生成 schedule）

  void jerasure_schedule_encode(int k, int m, int w, int **schedule, char **data_ptrs, char **coding_ptrs, int size, int packetsize)

解码

• 常规有限域内的解码函数

  jerasure_matrix_decode(int k, int m, int w, int *matrix, int row_k_ones, int *erasures, char **data_ptrs, char **coding_ptrs, int size)

• 二进制矩阵下的解码函数

  jerasure_bitmatrix_decode(int k, int m, int w, int *bitmatrix, int row_k_ones, int *erasures,char **data_ptrs, char **coding_ptrs, int size, int packetsize)

  ---

• 使用解码矩阵（二进制）转换得到的 schedule 的解码函数（内部自动生成计划表，一步完成所有的解码操作，所有称作 lazy）

  int jerasure_schedule_decode_lazy(int k, int m, int w, int *bitmatrix, int *erasures,char **data_ptrs, char **coding_ptrs, int size, int packetsize,int smart)

• 上面一个函数关于 m=2 的优化，需要先生成所有可能（任意的 1｜2 个失效）的计划表

  int jerasure_schedule_decode_cache(int k, int m, int w, int ***scache, int *erasures,char **data_ptrs, char **coding_ptrs, int size, int packetsize)

工具函数

• 生成奇偶校验的函数

• 【灵活的】有限域向量与编码块做点积、【灵活的】二进制超行(w*kw)与编码块(kw 个 packets)做点积，用于通常的编码函数 jerasure_matrix_encode | jerasure_bitmatrix_encode

• 有限域矩阵求逆｜判断可逆、二进制矩阵求你｜判断可逆、矩阵乘法、矩阵转位矩阵

• 返回通常的 有限域｜二进制解码矩阵（前 k 个有效块 对应的行|超行 的逆矩阵），用于常规的解码函数 jerasure_matrix_decode | jerasure_bitmatrix_decode

调试和统计

• 打印矩阵

  void jerasure_print_matrix(int *m, int rows, int cols, int w)

  void jerasure_print_bitmatrix(int *m, int rows, int cols, int w)

• 统计运算

  void jerasure_get_stats(double *fill_in)

notes

• $jerasure\_schedule\_decode\_lazy$ 生成解码矩阵的过程，求逆矩阵是 $O(n^3)$ 级别

参考链接

1. Jerasure: A Library in C/C++ Facilitating Erasure Coding for Storage Applications. Version 1.2
2. 【1】的翻译 探秘 Jerasure
3. 博客-JErasure库的相关学习
4. 部分源代码和注释在线阅读参考